Что бывает треугольной формы для детей — Детки-конфетки
Главная > Развивайка >
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.

Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Содержание статьи
Содержание статьи:
Нескучная геометрия
Геометрия — это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми — удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.

Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг
Круг — самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг — это шар (мячик, клубок)

Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат
Квадрат — это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы — кубики, коробки, дом, окно, подушка, табурет и т. п.

Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник
Прямоугольник — родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.

Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
Треугольник
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.

В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал
Овал — это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.

Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов — эллипсовидная.
Ромб
Ромб — тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.

Изучать ромб можно с помощью наглядных пособий — нарисованной картинки или объемного предмета.
Приемы запоминания
 Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
- Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.
- Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор — очень много интересных сочетаний можно выложить, комбинируя разные фигурки.
 Приобретите деревянные или пластиковые объемные математические фигуры в магазине для детей.
Приобретите деревянные или пластиковые объемные математические фигуры в магазине для детей.- Хорошо увлекают малышей сортеры, в которых нужно в отверстия вставлять подходящие геометрические фигуры из комплекта.
- Купите линейку с отверстиями в форме круга, квадрата, треугольника и других — для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки — интереснейшее занятие.
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Понравилась статья? Поделитесь с друзьями!
Source: RazvitieMalysha.ruЧитайте также
Виды треугольников (по сторонам). Видеоурок. Математика 3 Класс
На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
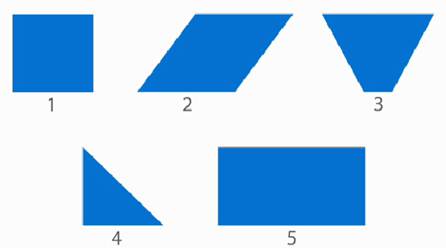
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 – четырехугольники. Каждая из них имеет свое название (рис. 2).
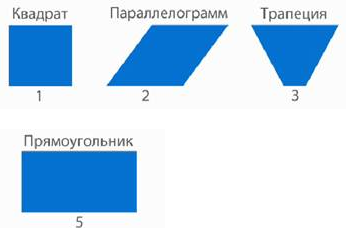
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
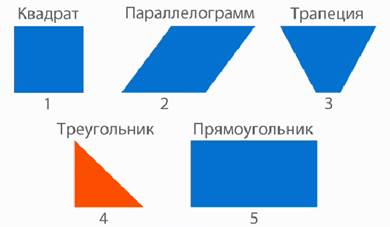
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника, отрезки – его сторонами. Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
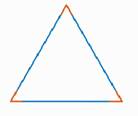
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
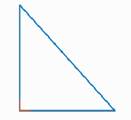
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
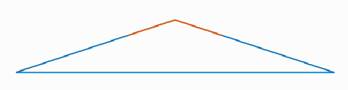
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
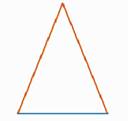
Эти стороны называются боковыми, третья сторона – основанием. В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
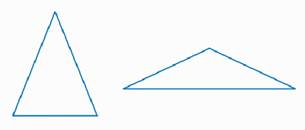
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).

Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны. Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).

Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
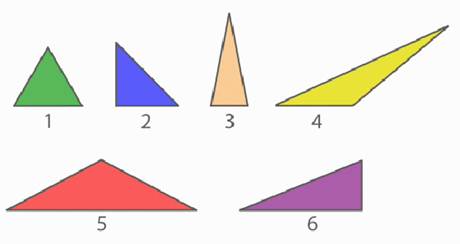
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
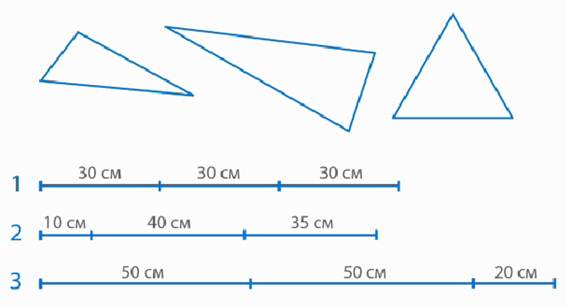
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Nsportal.ru (Источник).
- Prosv.ru (Источник).
- Do.gendocs.ru (Источник).
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются …, отрезки – его …. Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
interneturok.ru
Какие предметы треугольной формы Вы знаете?
Двускатная крыша дома. Шале.
Треуголку Наполеона Бонапарта.))
Треугольник, поза в йоге, стол, окно, значок папок (в Windows), инструмент игральный (вроде называется треугольнички) , нос, одежда, выключатель/включатель, кнопка. Что-то больше не припомлнилось.:)
…у меня есть сережки-треугольники: -)))))
Творчество в психологии определяется треугольниками)))
Ячейка жесткой конструкции, наконечник стрелы, современный самолет, любовный треугольник…
голова Ясписа, лапоть, баян.
touch.otvet.mail.ru
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
 Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
 Разносторонний треугольник — все три стороны не равны.
Разносторонний треугольник — все три стороны не равны.
 Равнобедренный треугольник — две стороны равны.
Равнобедренный треугольник — две стороны равны.
 Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
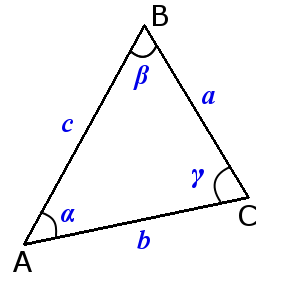
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
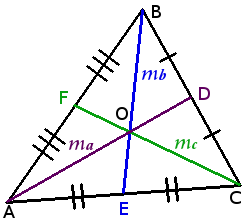
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
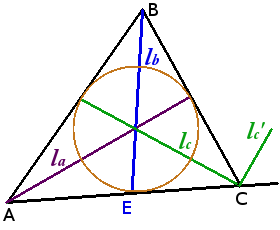
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
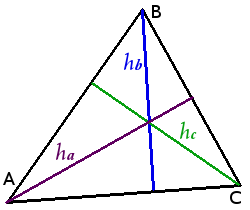
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
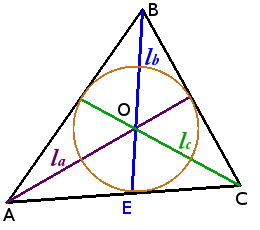
Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
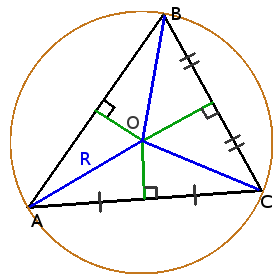
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр вписанной в треугольник окружности лежит на пересечении серединных перпендикуляров к уго сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.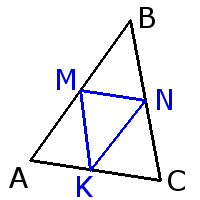 Средняя линия треугольника параллельна основанию и равна его половине.
Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
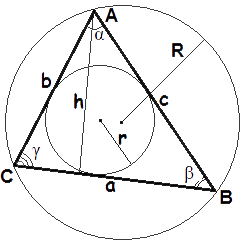
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника. - Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
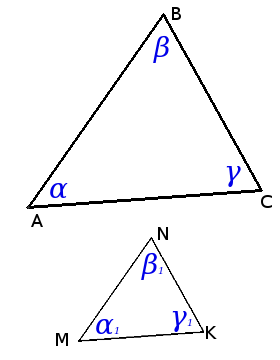 Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
ru.onlinemschool.com
Как определить тип лица и как с ним жить
Какие формы лица существуют
 makefor.me
makefor.me- Овальное лицо: лоб чуть шире нижней челюсти, выражены скулы, лицо мягко сужается к подбородку.
- Круглое лицо: длина и ширина лица примерно равны, широкие скулы, относительно низкий лоб и узкая челюсть.
- Прямоугольное лицо: высокий и ярко выраженный лоб, удлинённый подбородок, широкие скулы.
- Квадратное лицо: равные высота и ширина лица, низкий лоб и широкие скулы, выраженная линия челюсти.
- Треугольное лицо: широкие линии лба и скул, узкий подбородок.
- Грушевидное лицо: широкая челюсть, линия лба короче линии скул.
- Ромбовидное лицо: широкие скулы и равные по длине линии лба и челюсти.
Как определить свой тип лица
Способ первый
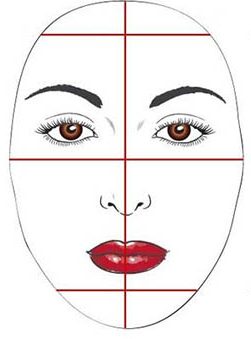
Нам понадобится большое зеркало, фломастер или маркер (лучше, чтобы он хорошо отмывался). Уберите волосы с лица и подойдите к зеркалу. Не забудьте выпрямить спину и расправить плечи. Смотря прямо перед собой, обведите фломастером контур своего лица, не учитывая уши и объём волос. При этом старайтесь не двигаться, чтобы рисунок получился максимально точным. Закончили? Отойдите в сторону, и оцените получившуюся фигуру.
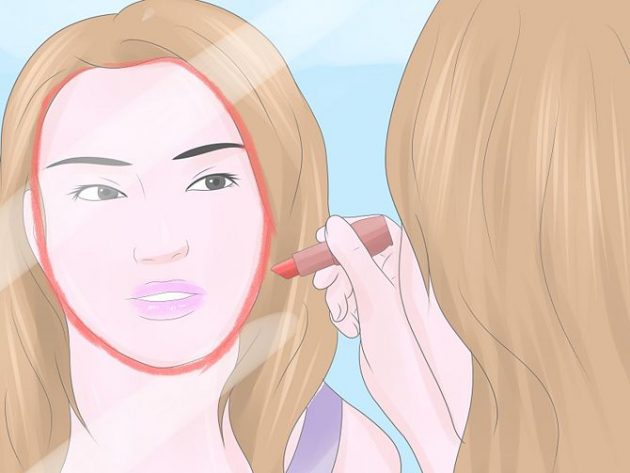 blogspot.com
blogspot.comСпособ второй
Замерьте сантиметром лоб, скулы и челюсти в самой широкой части, а также расстояние от лба до подбородка по вертикали. Сравните получившиеся показатели: какая линия самая широкая? какая самая узкая? насколько лицо длиннее по вертикали, чем по горизонтали? Соотнесите ответы с описанием каждого типа лица.
 lokoni.com
lokoni.comПомните, что лицо, идеально вписывающееся в определённую форму, можно встретить редко. Чаще попадаются вариации основных семи типов. Определите, какая форма максимально приближена к вашей, и следуйте рекомендациям избирательно.
Овальное лицо
 Звёзды с овальными лицами: Синди Кроуфорд, Гвинет Пэлтроу, Шарлиз Терон
Звёзды с овальными лицами: Синди Кроуфорд, Гвинет Пэлтроу, Шарлиз ТеронСчитается идеалом. Корректируя прочие формы лица, мы будем стремиться именно к овальным контурам. Счастливым обладательницам личика-овала подойдут любые стрижки и укладки, можно спокойно экспериментировать с макияжем и изгибом бровей. В рамках разумного, само собой.
Круглое лицо
 Обладательницы круглых лиц: Кирстен Данст, Дрю Бэрримор, Кристина Риччи
Обладательницы круглых лиц: Кирстен Данст, Дрю Бэрримор, Кристина РиччиЕсли у вас именно такая форма лица, поздравляем! Вы будете выглядеть моложе намного дольше своих сверстниц. Мягкие, плавные черты круглого лица придают нежность и женственность вашей внешности. Но чтобы выглядеть ещё лучше, нужно гармонизировать контур лица: визуально вытянуть его по вертикали.
Причёски
Вам подойдут:
- Распущенные прямые волосы, выпущенные по бокам прядки. Они скроют скулы и щёки.
- Объём или начёс на макушке зрительно удлинит лицо.
- Косая чёлка, косой пробор, асимметричная стрижка отвлекут внимание от округлостей.
- Мягкие волны, начинающиеся ниже линии подбородка, если вам хочется завить волосы.
Не подойдут:
- Полностью убранные в высокий пучок или хвост волосы. Это привлечёт внимание к открытым щекам.
- Объёмные пышные причёски и крупные локоны выше линии подбородка. Они визуально расширят скулы и щёки.
- Закруглённые стрижки вроде каре сделают лицо более круглым.
- Прямые чёлки уменьшат лоб и сплюснут лицо.
Форма бровей
На лице круглой формы лучше всего будут смотреться короткие брови с высоким подъёмом. Длинные тонкие брови могут добавить лишней ширины.
Макияж
При нанесении макияжа уделяйте особое внимание затемнению висков и области под скулами. Не перебарщивайте со светлыми оттенками под глазами и в верхней части скул.
Прямоугольное лицо
 Знаменитые прямоугольные лица: Коби Смолдерс, Сандра Буллок, Энди Макдауэлл
Знаменитые прямоугольные лица: Коби Смолдерс, Сандра Буллок, Энди МакдауэллПрямоугольная (также её называют вытянутой) форма лица похожа на овальную, но с более выраженными скулами и высоким лбом. Чтобы уравновесить прямоугольник, надо сгладить резкие углы, зрительно уменьшить линию «лоб — подбородок» и расширить скулы.
Причёски
Вам подойдут:
- Градуированная стрижка или локоны по контуру лица. Это смягчит черты.
- Кудри в районе скул или расширенное по бокам каре. Это поможет увеличить линию скул.
- Филированная или густая чёлка до бровей скроет высокий лоб.
- Волосы длиной чуть ниже подбородка. Это поможет расширить узкое вытянутое лицо.
Не подойдут прямые распущенные по бокам или зачёсанные назад волосы, а также высокие причёски с начёсом. Они ещё больше вытянут лицо.
Форма бровей
Бровям придайте горизонтальную форму. Это визуально расширит контур лица.
Макияж
Можете воспользоваться маленькой хитростью: подберите два тональных крема, один на тон темнее другого. Затемняйте области лба и подбородка, а более светлый оттенок наносите на среднюю часть лица. Не забудьте хорошо растушевать основу, не оставляя резкого цветового перехода. Напоследок выделите верхнюю часть скул, добавив немного хайлайтера.
Квадратное лицо
 Звёзды с квадратными лицами: Пэрис Хилтон, Оливия Уайлд, Хелена Бонэм Картер
Звёзды с квадратными лицами: Пэрис Хилтон, Оливия Уайлд, Хелена Бонэм КартерЖенщины, относящиеся к этому типу, могут гордиться своими красивыми скулами и чёткой линией подбородка. А чтобы выглядеть наилучшим образом, достаточно зрительно вытянуть вертикаль лица и смягчить его черты.
Причёски
Вам подойдут:
- Причёски с мягкими и плавными линиями и переходами цветов.
- Нежные закруглённые локоны и завитки, уложенные по сторонам лица.
- Мягкая асимметричная чёлка или чёлка, уложенная набок. Она визуально смягчит и отвлечёт внимание от тяжёлого подбородка.
- Длинные прямые волосы удлинят лицо и скроют резкие скулы.
- Объём или начёс на макушке поднимет лоб и вытянет вертикаль «лоб — подбородок».
Не подойдут:
- Прямые линии в стрижке: ваше лицо и так богато чёткими линиями, не стоит перегружать образ.
- Волосы по подбородок и выше, особенно подстриженные по линейке, акцентируют внимание на подбородке и утяжеляют его, а также добавляют лишний объём скулам.
- Прямая длинная или короткая чёлка скроет лоб и укоротит лицо.
Форма бровей
Не забывайте о грамотной коррекции бровей: выбирайте закруглённую форму или горизонтальную вразлёт.
Макияж
Пользуйтесь простым приёмом: высветляйте лицо по центральной вертикали (середина лба — нос — середина подбородка) и слегка затемняйте по краям (стороны лба — виски — скулы).
Треугольное лицо
 Звёзды с лицом сердечком: Скарлетт Йоханссон, Риз Уизерспун, Виктория Бекхэм
Звёзды с лицом сердечком: Скарлетт Йоханссон, Риз Уизерспун, Виктория БекхэмШирокий и высокий лоб обычно считают признаком ума. А если у вас треугольная форма лица, то можно гордиться и привлекательным заострённым подбородком. И всё же мы стремимся к овалу, помните? А потому наша цель — визуально сузить самую широкую линию, линию лба.
Причёски
Вам подойдут:
- Причёски с объёмом ниже линии скул (в идеале, чтобы самая широкая часть находилась на уровне подбородка). Это мгновенно уравновесит верхнюю часть лица.
- Широкие прямые или косые чёлки.
- Волосы любой длины с прядками, закругляющимися к подбородку: они зрительно его расширят. Идеальная для вас длина — ниже подбородка и выше плеч.
- Из коротких стрижек лучше всего будет смотреться удлинённый асимметричный боб.
Не подойдут:
- Объём в верхней части головы. Начёсы, выделенные прядки, зачёсанная чёлка, крутые локоны у висков утяжелят лоб.
- Укладки от лица. Они откроют ваши изящные скулы и подбородок, усилив диспропорцию.
- Короткие стрижки, открывающих лицо полностью.
Форма бровей
Хорошо будут выглядеть закруглённые дугообразные брови. Они отвлекут внимание от узкого подбородка.
Макияж
В ежедневном макияже достаточно будет лишь чуть-чуть затемнить кончик подбородка и лоб по краям.
Грушевидное лицо
 Обладательницы грушевидных лиц: Келли Осборн, Рене Зеллвегер, Куин Латифа
Обладательницы грушевидных лиц: Келли Осборн, Рене Зеллвегер, Куин ЛатифаПо-другому такой контур можно назвать перевёрнутым треугольником. С помощью волос, коррекции бровей и макияжа мы будем расширять линию лба и сужать подбородок.
Причёски
Вам подойдут:
- Объём на макушке, поднятая чёлка и начёсы сыграют на руку и уравновесят тяжесть нижней части лица.
- Боковой косой пробор отвлечёт от вертикали лица и подбородка.
- Высокий пышный пучок с небрежно выпущенными прядями сосредоточит взгляд на верхней части головы.
- Косая удлинённая чёлка уравновесит лоб и подбородок.
- Завитые ниже подбородка локоны с объёмом выше висков тоже прекрасно подойдут.
Не подойдут:
- Высоко убранные волосы (конский хвост, гладкий пучок) акцентируют внимание на тяжести нижней части лица.
- Объём на уровне скул или подбородка визуально сделает лоб более узким.
- Прямой пробор — ровная линия посередине лица — излишне выделит нос и подбородок.
Форма бровей
Отлично вытянут лоб удлинённые горизонтальные брови.
Макияж
С помощью тона или хайлайтера слегка высветляйте верхнюю часть лица.
Ромбовидное лицо
 Звёзды с ромбовидными лицами: Тейлор Свифт, Лиза Кудроу, Софи Лорен
Звёзды с ромбовидными лицами: Тейлор Свифт, Лиза Кудроу, Софи ЛоренФорму лица в виде ромба зачастую именуют алмазной. От овальной она отличается более узким лбом и подбородком и выдающимися скулами. А значит, надо расширить верхнюю часть лица, отвлечь внимание от средней и скрыть излишнюю длину.
Причёски
Вам подойдут:
- Косая удлинённая чёлка и боковой пробор. Это зрительно увеличит лоб и уменьшит вытянутость лица.
- Объём выше висков и ниже скул позволит уравновесить выдающиеся скулы.
- Пышная чёлка, уложенная прямо или набок, укоротит вытянутую вертикаль лица.
- Высокие пышные укладки с оставленными вдоль скул прядками расширят линию лба и сгладят скулы.
Не подойдут:
- Объём на уровне скул дополнительно расширит среднюю часть лица.
- Прямой пробор зрительно увеличит длину лица.
- Короткие стрижки выше подбородка (особенно без чёлки) подчеркнут его хрупкость и усилят перевес в сторону скул.
- Гладкая плоская чёлка сделает верхнюю часть лица меньше.
- Излишний объём на макушке визуально удлинит лицо по вертикали.
Форма бровей
Девушкам с алмазным лицом стоит попробовать брови с подъёмом и недлинными кончиками.
Макияж
В макияже достаточно сгладить корректором тёмного цвета боковые части скул.
Каждое лицо красиво и неповторимо. Знайте свои особенности и умейте не только их скрывать, но и выгодно подчёркивать. Иногда можно следовать рекомендациям с точностью до наоборот, чтобы выделить уникальность черт своего лица.
lifehacker.ru
Что такое треугольник Рёло ?
Треуголник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур (как круг), обладающих постоянной шириной. То есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины.
По мнению историков, название это «непростой» простой фигуре дал немецкий механик Франц Рёло, живший с 1829 по 1905 годы. Многие историки сходятся в том, что именно он стал первооткрывателем свойств этой геометрической фигуры. Потому как он первый широко использовал свойства и возможности треугольника Рёло в своих механизмах.
Франц Рёло первым дал доскональные определения понятиям «кинетическая пара», «кинетическая цепь». Он впервые показал возможность связи между основами механики и конструирования. То есть связал теорию и практические проблемы конструирования. Что позволило создавать механизмы в совокупности их функциональных возможностей с внешней привлекательностью/эстетичностью. Отсюда Рёло стали считать поэтом механики. Что позволило последователям в корне пересмотреть имеющиеся в ней теории.
Иные исследователи первооткрывателем этой фигуры признают Леонарда Эйлер (18 век), который уже тогда продемонстрировал возможность его создания ее из трех окружностей.
А третьи «увидели» треугольник Рёло в рукописях гениального Леонардо Да Винчи. Манускрипты этого естествоиспытателя, с изображением этой «простой» фигуры, хранятся в Мадридском кодексе и в Институте Франции.
Но кто бы ни был первооткрывателем этот «не простой» треугольник получил широкое распространение в современном мире.
А именно:
• Сверло Уаттса. В 1914 году Гарри Джеймс Уаттс изобрел уникальный инструмент для высверливания квадратных отверстий. Это сверло, выполнено в форме Треугольника Рёло;
• Двигатель Ванкеля. С 1957 года треугольник Рёло немецкий изобретатель Ванкель Ф. создал уникальный механизм. Где внутри камеры, цилиндрической формы, по сложной траектории передвигается ротор-поршень. Созданный в форме треугольника Рёло. При его постоянном движении, каждая его грань, контактируя со стенками камеры, образует сразу три камеры, названные позже «камерами сгорания».
Вот тут можно вспомнить подробный пост про двигатель Ванкеля
• Грейферный механизм кинопроекторов. Треугольник Рёло, вписанный в квадрат и двойной параллелограмм лежат в его основе. А нужен он для равномерного продергивания кинопленки во время киносеанса со скоростью в 18 кадров/с без отклонений и задержек;
• Основа кулачкового механизма для зигзагообразного шва в швейных машинках, а также в немецких часах таких известных марок как A. Lange & Söhne «Lange 31»;
• Плектр или медиатор, тоже не что иное, как треугольник Рёло. Они необходимы при игре на щипковых музыкальных инструментах.
• В архитектуре. Конструкция из двух дуг треугольника Рёло образует стрельчатую арку готического стиля. А окна в форме Рёло стоят в Брюгге в церкви Богоматери. Как орнамент он присутствует и на оконных решетках швейцарской коммуны Отрив и цистерцианского аббатства.
На самом деле Рёло не является первооткрывателем этой фигуры, хотя он и подробно исследовал её. В частности, он рассматривал вопрос о том, сколько контактов (в кинематических парах) необходимо, чтобы предотвратить движение плоской фигуры, и на примере искривлённого треугольника, вписанного в квадрат, показал, что даже трёх контактов может быть недостаточно для того, чтобы фигура не вращалась.
Леонардо да Винчи, манускрипт A, фрагмент листа 15v
Некоторые математики считают, что первым продемонстрировал идею треугольника из равных дуг окружности Леонард Эйлер в XVIII веке. Тем не менее, подобная фигура встречается и раньше, в XV веке: её использовал в своих рукописях Леонардо да Винчи. Треугольник Рёло есть в его манускриптах A и B, хранящихся в Институте Франции[10], а также в Мадридском кодексе.
Примерно в 1514 году Леонардо да Винчи создал одну из первых в своём роде карт мира. Поверхность земного шара на ней была разделена экватором и двумя меридианами(угол между плоскостями этих меридианов равен 90°) на восемь сферических треугольников, которые были показаны на плоскости карты треугольниками Рёло, собранными по четыре вокруг полюсов.
Ещё раньше, в XIII веке, создатели церкви Богоматери в Брюгге использовали треугольник Рёло в качестве формы для некоторых окон
Следовательно, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства, как характеристики простой фигуры, находится в постоянном теоретическом и практическом изучении.
Именно треугольник Рело может помочь нам в сверлении квадратных отверстий. Достаточно двигать центр этого «треугольника» по некой траектории, и его вершины начертят почти квадрат, а границы полученной фигуры, за исключением небольших кусочков по углам, будут строго прямыми! Такими, что, если продолжить отрезки, тем самым добавив уголочки, то получится в точности квадрат.Площадь незаметенных уголочков составляет всего около 2 процентов от площади всего квадрата!
А вот еще применение :
Китайский офицер Гуан Байхуа из Циндао заново изобрел колесо. Он создал необычный велосипед: вместо круглых колес у него треугольник сзади и пятиугольник спереди.
Сам изобретатель уверен, что новая модель будет пользоваться популярностью, поскольку, чтобы передвигаться на таком велосипеде, требуется больше усилий, а значит, это в какой-то степени может заменить спортивную нагрузку.
Добровольцы, опробовавшие новинку, были удивлены тем, насколько ровно передвигается велосипед с новыми колесами. Дело в том, что углы многоугольников сглажены. Это позволяет велосипеду не «прыгать» вверх-вниз, как можно было бы ожидать, поясняет со ссылкой на The Times InoPressa.ru.
Кроме того, колеса по форме являются кривыми постоянной длины, иначе называемыми «многоугольниками Рело» или «круглыми многоугольниками». Контур таких фигур представляет собой плоскую выпуклую кривую, расстояние между любыми двумя параллельными опорными прямыми которой постоянно и равно «ширине» кривой.
Несмотря на то, что новый велосипед не пользуется коммерческим успехом, Байхуа не унывает. Теперь он занят созданием новой социальной сети в интернете.
Вот еще такое применение:
[источники]
источник
http://funnymath.ru/itsinteresting/other/273-treugolnik-rjolo
http://www.terrakid.ru/nash-blog/interesnye-izobreteniya-detej-i-vzroslykh-iz-raznykh-stran/129-chto-takoe-treugolnik-relo-ili-kak-sverlit-kvadratnye-otverstiya
http://www.newsru.com/world/27may2009/velo.html
https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA_%D0%A0%D1%91%D0%BB%D0%BE
Давайте я вам еще что нибудь напомню математического : вот например Самое большое число в мире и Как выиграть в игру «Орел или решка» !. А знаете, что я вам еще напомню про числа ? Вот например существует число «ФИ» , а вот волшебные ЧЕТЫРЕ ЧЕТВЕРКИ. Я вам еще рассказывал вот про такое удивительное число Шенона, ну и еще к нашей теме можно отнести закон Бенфорда и такое известие, что оказывается великая теорема Ферма ДОКАЗАНА Оригинал статьи находится на сайте ИнфоГлаз.рф Ссылка на статью, с которой сделана эта копия — http://infoglaz.ru/?p=69422
masterok.livejournal.com
Как узнать, какие прически будут вам к лицу, а про какие лучше забыть

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Каждая из нас мечтает об идеальной прическе, которая выгодно подчеркнет все достоинства лица и скроет недостатки. Сейчас существует такое разнообразие стилей, что трудно определиться с выбором, к тому же стало очень модно следовать трендам, хочется попробовать на себе новую «стрижку сезона», «цвет сезона» и т. п. На картинке они смотрятся отлично, а вот в реальной жизни могут сильно разочаровать. Как подобрать такую повседневную прическу, о которой не придется пожалеть, и расскажет наша статья.
Мы в AdMe.ru собрали типичные ошибки в выборе прически и рассмотрели их на примерах звезд. Самый главный совет, который в один голос повторяют все стилисты: не забывайте про форму своего лица. Форма решает все. В конце статьи вы найдете общие рекомендации о том, какие еще особенности внешности нужно обязательно учитывать перед походом в парикмахерскую.
Круглое лицо
Прямой пробор и гладкие убранные назад волосы не только подчеркивают широкое лицо Миранды Керр, но и прибавляют ей возраста. Зато удлиненный многослойный боб делает ее очаровательной.
Что не подходит: «Прически с пышным объемом по бокам, гладкие прически с убранными назад волосами и ровная линия среза возле подбородка или выше — это большая ошибка для круглого лица», — объясняет старший стилист в салоне Redken Даниэла Шульт. Также не подойдут прямой пробор и тяжелая густая челка. Эти прически лишь подчеркнут большую ширину вашего лица.
Что нужно взять на вооружение: Задача — визуально удлинить лицо. С этим прекрасно справятся прямые пряди у лица, текстурированная рваная челка, волны и многослойные стрижки на волосы средней длины или длинные. «Создавая многослойность, вы в конечном счете влияете на форму вашего лица — круглые лица должны выбирать квадратные слои», — говорит Сэм Бернетт, креативный директор компании Hare & Bone. Смелые круглолицые красавицы могут рискнуть и попробовать короткую стрижку пикси, как у Джиннифер Гудвин. Примеры удачных укладок и другие хитрости для круглого лица можно посмотреть здесь.
Квадратное лицо
Каре-боб длиной до подбородка привлекает внимание к широкой квадратной челюсти Оливии Уайлд. В обрамлении длинных волос лицо смотрится мягче и миловиднее.
Что не подходит: Чересчур графичные, симметричные линии в прическе лишь подчеркнут угловатость этого лица. Каре-боб до подбородка с прямой густой челкой под запретом, так как такая прическа лишь подчеркнет широкую нижнюю челюсть. С короткими стрижками тоже стоит быть аккуратнее — в данном случае они придадут лицу мужеподобность. «Девушки с квадратной формой лица должны избегать причесок, где волосы убраны назад, например гладко зачесаны назад в хвост. Это подчеркивает угловатые черты и делает их более жесткими», — отмечает Карен Томсон, стилист и владелец салона красоты.
Что нужно взять на вооружение: «Длинные волосы особенно хороши для квадратного лица, будь то прямые и гладкие, кудри или небрежные волны, они будут отвлекать внимание от угловатых краев лица. Если вы хотите челку, то лучше выбрать длинную челку набок, а не прямую, от которой лицо кажется еще шире», — советует Карен Томпсон. «Одна из моих любимых стрижек для данной формы лица — это удлиненный боб с косой челкой. Также очень хорошо смягчают углы легкие светлые блики на прядях возле лица», — говорит Даниэла Шульт. Варианты причесок, идеальных для лица квадратной формы, можно посмотреть здесь.
Треугольное и сердцевидное лицо

www.adme.ru

 Приобретите деревянные или пластиковые объемные математические фигуры в магазине для детей.
Приобретите деревянные или пластиковые объемные математические фигуры в магазине для детей. Остроугольный треугольник — все углы треугольника острые.
Остроугольный треугольник — все углы треугольника острые.
 Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
 Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
 Равнобедренный треугольник — две стороны равны.
Равнобедренный треугольник — две стороны равны.
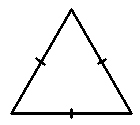 Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.