На силу – комплекс упражнений для увеличения возможности мышц, массы и выносливости в тренажерном зале и домашних условиях

СИЛА — это… Что такое СИЛА?

1. Величина, являющаяся мерой механического взаимодействия тел, вызывающего их ускорение или деформацию; характеристика интенсивности физических процессов (спец.). Единица силы. Центробежная с. С. тяжести. С. тока. С. света. С. инерции. С. ветра. Землетрясение силой в шесть баллов.

2. Способность живых существ напряжением мышц производить физические действия, движения; вообще физическая или моральная возможность активно действовать. Большая с. в руках. Толкнуть с силой. Нет больше сил. Это свыше моих сил. Лишиться сил. Выбиться из сил. Собраться с силами. Приняться за работу со свежими силами. Применить силу (физическое воздействие). Силой заставили (насильно). Действовать убеждением, а не силой. Политика с позиции силы (об агрессивной политике).

3. обычно мн. Материальное или духовное начало как источник энергии, деятельности. Силы природы. Творческие силы народа.

4. чего. Способность проявления какой-н. деятельности, состояния, отличающаяся определённой степенью напряжённости, устремлённости. С. воли. С. воображения.

5. Могущество, влияние, власть. Могучая с. слова. С. убеждения. Непобедимая с. народа.

6. Сущность, смысл (разг.). Вся с. в том, что он знает это лучше меня.

7. Действенность, правомочность (закона, решения, правила). Закон вступил в силу. Закон обратной силы не имеет. Старое решение потеряло (утратило) силу.

8. мн. Общественная группа, общественный слой, а также вообще люди, обладающие какими-н. характерными для них признаками.

Соотношение классовых сил. Лучшие артистические силы. 9. мн. Вооружённые силы, а также различные их виды. Военно-морские силы. Военно-воздушные силы. Главные силы (основная часть воюющих войск). 10. ед. Большое количество, множество (прост.). Народу там с. 11. силами кого (чего), в знач. предлога с род. Используя кого-что-н., при помощи кого-чего-н. Построено силами студентов. • В силах 1) в состоянии, может что-н. делать, активно действовать. Пока в силах, буду трудиться; 2) с неопред., мочь, располагать возможностью. Никто не в силах повлиять на него. В силе (разг.) в таком состоянии, когда есть власть, влияние. Этот человек сейчас в большой силе. В силу чего, предл. с род. (книжн.) по причине чего-н., из-за чего-н. Не смог явиться в силу сложившихся обстоятельств. В силу того что, союз (книжн.) из-за того что, по причине того что. Ответ задерживается, в силу того что отсутствуют необходимые сведения.

Изо всей силы или изо всех сил применяя всю свою силу, энергию. Старался из всех сил.

От силы (разг.) самое большее. Отсюда до города от силы тридцать километров. Весит от силы десять килограмм.

По силам, по силе или под силу кому соответствует чьим-н. возможностям, силам.

По силе возможности (прост.) по мере возможности. Помогает по силе возможности.

Своими силами самостоятельно, без посторонней помощи.

Сил нет (разг.) очень, чрезвычайно. Сил нет, как он мне надоел. Силою в (до, от… до…), в знач. предлога с вин. и род. в количестве, численностью. Отряд силою в пятьсот штыков (до пятисот штыков, от четырёхсот до пятисот штыков).

Силою вещей по причине сложившихся обстоятельств. Так получилось силою вещей.

Через силу сверх имеющихся возможностей, сил. Делать что-н. через силу.

Что есть силы (разг.) применяя всю свою физическую силу. Толкнул что есть силы. | прил. силовой, -ая, -ое (к 1 и 2 знач.). Силовое поле (спец.). С. приём. Силовая борьба. Силовое решение (волевое). Силовые министерства (уполномоченные в необходимых случаях на силовые воздействия, на применение оружия).

Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949-1992.

Сила (физическая величина) — это… Что такое Сила (физическая величина)?

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.

[1]

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами.В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).

[2].

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе.

При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями.

[3]^[4][5][6]

С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.^[3] Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия.^[7]

Размерность силы — LMT⁻², единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.

История понятия

Понятие силы использовали ещё ученые античности в своих работах о статике и движении. Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед.^[8] Представления Аристотеля о силе, связанные с фундаментальными несоответствиями, просуществовали в течение нескольких столетий. Эти несоответствия устранил в XVII в. Исаак Ньютон, используя для описания силы математические методы. Механика Ньютона оставалась общепринятой на протяжении почти трехсот лет.^[5] К началу XX в. Альберт Эйнштейн в теории относительности показал, что ньютоновская механика верна лишь в при сравнительно небольших скоростях движения и массах тел в системе, уточнив тем самым основные положения кинематики и динамики и описав некоторые новые свойства пространства-времени.

Ньютоновская механика

Исаак Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (знаменитые законы Ньютона).^[5][9]

Первый закон Ньютона

Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.

[9] Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.

[10]

Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скоростью и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга.

Второй закон Ньютона

Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.

где − импульс материальной точки, − суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки.^[9]

По определению импульса:

где − масса, − скорость.

По правилу нахождения производной произведения:

Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид:

Учитывая определение ускорения точки, второй закон Ньютона принимает вид:

Считается, что это «вторая самая известная формула в физике»^[11], хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна .

Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.

Третий закон Ньютона

Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2.^[12] Математически закон записывается так:

Этот закон означает, что силы всегда возникают парами «действие-противодействие».^[9] Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.^[3]

Фундаментальные взаимодействия

Все силы в природе основаны на четырех типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные − между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.

Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется берущей из античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».

Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящими через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово сила, заменяя его словом взаимодействие.^[13]

Каждый вид взаимодействия обусловлен обменом соответствующих переносчиков взаимодействия: гравитационное − обменом гравитонов (существование не подтверждено экспериментально), электромагнитное − виртуальных фотонов, слабое − векторных бозонов, сильное − глюонов (и на больших расстояниях — мезонов). В настоящее время электромагнитное и слабое взаимодействия объединены в более фундаментальное электрослабое взаимодействие. Делаются попытки объединения всех четырех фундаментальных взаимодействие в одно (так называемая теория великого объединения).

Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к этим четырем фундаментальным взаимодействиям. Например, трение − это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули,^[14] который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решетки вещества удерживаться около положения равновесия.^[3].

Однако на практике оказывается не только нецелесообразной, но и просто невозможной по условиям задачи подобная детализация рассмотрения вопроса о действии сил.

Гравитация

Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Исааком Ньютоном в его труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчете, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел^[15]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой , прямо пропорциональной произведению масс ( и ) и обратно пропорциональной квадрату расстояния между ними:

Здесь − гравитационная постоянная^[16], значение которой впервые получил в своих опытах Генри Кавендиш. Используя данный закон, можно получить формулы для расчета силы тяготения тел произвольной формы. Теория тяготения Ньютона хорошо описывает движение планет Солнечной системы и многих других небесных тел. Однако, в ее основе лежит концепция дальнодействия, противоречащая теории относительности. Поэтому классическая теория тяготения неприменима для описания движения тел, перемещающихся со скоростью, близкой к скорости света, гравитационных полей чрезвычайно массивных объектов (например, черных дыр), а также переменных полей тяготения, создаваемых движущимися телами, на больших расстояниях от них^[17].

Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривленным траекториям в трехмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырехмерном пространстве-времени, в котором время в разных точках течет по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе^[3].

Электромагнитное взаимодействие

Электростатическое поле (поле неподвижных зарядов)

Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью C. Однако, исходя из требований практики, основанных на удобствах измерения, вместо заряда нередко стал использоваться электрический ток с размерностью I, причём I = CT ^{− 1}. Единицей измерения величины заряда является кулон, а силы тока ампер.

Поскольку заряд, как таковой, не существует независимо от несущего его тела, то электрическое взаимодействие тел проявляется в виде той же рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух «точечных зарядов» в вакууме используется закон Кулона:

где  — расстояние между зарядами, а ε₀ ≈ 8.854187817·10⁻¹² Ф/м. В однородном (изотропном) веществе в этой системе сила взаимодействия уменьшается в ε раз, где ε — диэлектрическая постоянная среды.

Направление силы совпадает с линией, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым бы перемещалась лишённая массы заряжённая частица. Эти линии начинаются на одном и заканчиваются на другом зарядах.

Электромагнитное поле (поле постоянных токов)

Существование магнитного поля признавалось ещё в средние века китайцами, использовавшим «любящий камень» — магнит, в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.

Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.

Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.

Ампер высказал гипотезу, признаваемую в физике, как модель процесса возникновения магнитного поля, заключающуюся в существовании в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.

Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции, лежащим в плоскости, расположенной перпендикулярно по отношению к направлению движения заряда.

Единицей измерения магнитной индукции является тесла: 1 Тл = 1 Т кг с⁻² А⁻²
Количественно задача была решена Ампером, измерявшим силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.

Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга описывается законом Кулона. Однако заряды, находящиеся в движении относительно друг друга создают магнитные поля, посредством которых созданные движением зарядов токов в общем случае приходят в состояние силового взаимодействия.

Принципиальным отличием силы, возникающей при относительном движении зарядов от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сил взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.

В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обоих токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.

Закон взаимодействия токов используется для эталонирования постоянного электрического тока.

Сильное взаимодействие

Сильное взаимодействие — короткодействующие силы между адронами и кварками. В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающее отталкивание, благодаря этому атомные ядра не «схлопываютс­я­».

Внутри самих адронов сильное взаимодействие удерживает вместе кварки — составные части адронов. Квантами сильного поля являются глюоны. Каждый кварк имеет один из трёх «цветовых» зарядов, каждый глюон состоит из пары «цвет»-«антицвет». Глюоны связывают кварки в т. н. «конфайнмент», из-за которого на данный момент свободные кварки в эксперименте не наблюдались. При отдалении кварков друг от друга энергия глюонных связей возрастает, а не уменьшается как при ядерном взаимодействии. Затратив много энергии (столкнув адроны в ускорителе) можно разорвать кварк-глюонную связь, но при этом происходит выброс струи новых адронов. Впрочем, свободные кварки могут существовать в космосе: если какому-то кварку удалось избежать конфайнмента во время Большого взрыва, то вероятность аннигилировать с соответствующим антикварком или превратиться в бесцветный адрон для такого кварка исчезающе мала.

Слабое взаимодействие

Слабое взаимодействие — фундаментальное короткодействующее взаимодействие. Радиус действия 10⁻¹⁸ м. Симметрично относительно комбинации пространственной инверсии и зарядового сопряжения. В слабом взаимодействии участвуют все фундаментальные фермионы (лептоны и кварки). Это единственное взаимодействие, в котором участвуют нейтрино (не считая гравитации, пренебрежимо малой в лабораторных условиях), чем объясняется колоссальная проникающая способность этих частиц. Слабое взаимодействие позволяет лептонам, кваркам и их античастицам обмениваться энергией, массой, электрическим зарядом и квантовыми числами — то есть превращаться друг в друга. Одно из проявлений — бета-распад.

Производные виды сил

Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила упругости направлена противоположно смещению, перпендикулярно поверхности. Вектор силы противоположен направлению смещения молекул.

Сила трения — сила, возникающая при относительном движении твёрдых тел и противодействующая этому движению. Относится к диссипативным силам. Сила трения имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы трения направлен противоположно вектору скорости.

Сила сопротивления среды — сила, возникающая при движении твёрдого тела в жидкой или газообразной среде. Относится к диссипативным силам. Сила сопротивления имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы сопротивления направлен противоположно вектору скорости.

Сила нормальной реакции опоры — сила упругости, действующая со стороны опоры на тело. Направлена перпендикулярно к поверхности опоры.

Силы поверхностного натяжения — силы, возникающие на поверхности фазового раздела. Имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила натяжения направлена по касательной к поверхности раздела фаз; возникает вследствие нескомпенсированного притяжения молекул, находящихся на границе раздела фаз, молекулами, находящимися не на границе раздела фаз.

Осмотическое давление

Силы Ван-дер-Ваальса — электромагнитные межмолекулярные силы, возникающие при поляризации молекул и образовании диполей. Ван-дер-Ваальсовы силы быстро убывают с увеличением расстояния.

Сила инерции — фиктивная сила, вводимая в неинерциальных системах отсчёта для того, чтобы в них выполнялся второй закон Ньютона. В частности, в системе отсчёта, связанной с равноускоренно движущимся телом сила инерции направлена противоположно ускорению. Из полной силы инерции могут быть для удобства выделены центробежная сила и сила Кориолиса.

Равнодействующая

При расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей. Это геометрическая сумма всех сил, действующих на тело. При этом действие каждой силы не зависит от действия других, то есть каждая сила сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил (принцип суперпозиции).

См. также

Источники

Примечания

1. ↑ Glossary. Earth Observatory. NASA. — «Сила — любой внешний фактор, который вызывает изменение в движении свободного тела или возникновение внутренних напряжений в зафиксированном теле.»  (англ.)
2. ↑ Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
3. ↑ ^{1 2 3 4 5} Feynman, R. P., Leighton, R. B., Sands, M. Lectures on Physics, Vol 1 — Addison-Wesley, 1963.  (англ.)
4. ↑ Kleppner, D., Kolenkow, R. J. An introduction to mechanics — McGraw-Hill.  (англ.)
5. ↑ ^{1 2 3} University Physics, Sears, Young & Zemansky, pp. 18-38  (англ.)
6. ↑ Хайкин С. Э.Силы инерции и невесомость. Изд-во «Наука» М.,1967, с илл.
7. ↑ Weinberg, S. Dreams of a Final Theory — Vintage Books USA, 1994. — ISBN 0-679-74408-8.  (англ.)
8. ↑ Heath,T.L. The Works of Archimedes (1897). Archive.org. Архивировано из первоисточника 23 августа 2011. Проверено 14 октября 2007.  (англ.)
9. ↑ ^{1 2 3 4} Newton, I. The Principia Mathematical Principles of Natural Philosophy — University of California Press, 1999. — ISBN 0-520-08817-4.  (англ.)
10. ↑ Мултановский В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика — М.: Просвещение, 1988. — С. 80−81.
11. ↑ Принято не подчёркивать специально, что в такой формулировке Второй закон Ньютона годится только для наблюдателя, имеющего достаточные основания считать, что он находится в инерциальной системе отсчёта, из которой он и наблюдает движущееся под действием силы тело. Если же он сам находится в системе отсчёта, связанной с ускоряемым телом, в которой оно для него неподвижно, то в этой ситуации Второй закон Ньютона принимает вид: F − ma = 0 . Или F − F(i) = 0 , где F(i) есть сила инерции, действующей на ускоряемое тело, уравновешивающая по Третьему закону Ньютона действующее на него силу, что является причиной неподвижности этого тела в рассматриваемой неинерциальной системе отсчёта. Сила инерции фиктивна в том смысле, что причиной её возникновения не являются, в конечном итоге, ни силы гравитации, ни силы электромагнитного происхождения. Она появляется исключительно из-за неинерциальности движения системы наблюдателя.
12. ↑ Henderson, Tom Lesson 4: Newton’s Third Law of Motion. The Physics Classroom (1996-2007). Архивировано из первоисточника 23 августа 2011. Проверено 4 января 2008.  (англ.)
13. ↑ Капра, Фритьоф ДАО ФИЗИКИ. СПб.,»ОРИС»*»ЯНА-ПРИНТ». 1994 г. 304 с. ISBN 5-88436-021-5
14. ↑ Nave, R Pauli Exclusion Principle. HyperPhysics***** Quantum Physics. Архивировано из первоисточника 23 августа 2011. Проверено 2 января 2008.  (англ.)
15. ↑ University Physics, Sears, Young & Zemansky, pp. 59−82  (англ.)
16. ↑ Sir Isaac Newton: The Universal Law of Gravitation. Astronomy 161 The Solar System. Архивировано из первоисточника 23 августа 2011. Проверено 4 января 2008.  (англ.)
17. ↑ Статья И. Д. Новикова Физический энциклопедический словарь — М.: Советская энциклопедия, 1984. — С. 772−775.

Сила — это… Что такое Сила?

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций.^[1]

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).^[2].

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе.

При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями.^[3][4][5][6]

С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное, сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.^[3] Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия.^[7]

Размерность силы — LMT⁻², единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.

История понятия

Понятие силы использовали ещё ученые античности в своих работах о статике и движении. Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед.^[8] Представления Аристотеля о силе, связанные с фундаментальными несоответствиями, просуществовали в течение нескольких столетий. Эти несоответствия устранил в XVII в. Исаак Ньютон, используя для описания силы математические методы. Механика Ньютона оставалась общепринятой на протяжении почти трехсот лет.^[5] К началу XX в. Альберт Эйнштейн в теории относительности показал, что ньютоновская механика верна лишь в при сравнительно небольших скоростях движения и массах тел в системе, уточнив тем самым основные положения кинематики и динамики и описав некоторые новые свойства пространства-времени.

Ньютоновская механика

Исаак Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (знаменитые законы Ньютона).^[5][9]

Первый закон Ньютона

Первый закон Ньютона утверждает, что существуют системы отсчета, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий.^[9] Такие системы отсчета называются инерциальными. Ньютон предположил, что каждый массивный объект имеет определенный запас инерции, который характеризует «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой физически неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить какие из них находится «в движении», а какие «покоятся». Говорить о движении можно лишь относительно какой-либо системы отсчета. Законы механики выполняются одинаково во всех инерциальных системах отсчета, другими словами все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея.^[10]

Прямолинейное равномерно ускоряющееся движение в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта.

Например, законы механики абсолютно одинаково выполняются в кузове грузовика, когда тот едет по прямому участку дороги с постоянной скоростью и когда стоит на месте. Человек может подбросить мячик вертикально вверх и поймать его через некоторое время на том же самом месте вне зависимости от того движется ли грузовик равномерно и прямолинейно или покоится. Для него мячик летит по прямой. Однако для стороннего наблюдателя, находящегося на земле, траектория движения мячика имеет вид параболы. Это связано с тем, что мячик относительно земли движется во время полета не только вертикально, но и горизонтально по инерции в сторону движения грузовика. Для человека, находящегося в кузове грузовика не имеет значения движется ли последний по дороге, или окружающий мир перемещается с постоянной скоростью в противоположном направлении, а грузовик стоит на месте. Таким образом, состояние покоя и равномерного прямолинейного движения физически неотличимы друг от друга.

Второй закон Ньютона

Хотя второй закон Ньютона традиционно записывают в виде: , сам Ньютон записывал его несколько иначе^[как?]

Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.

где − импульс материальной точки, − суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки^[9].

По определению импульса:

где − масса, − скорость.

В классической механике при скоростях движения много меньше скорости света масса материальной точки считается неизменной, что позволяет выносить её при этих условиях за знак дифференциала :

Учитывая определение ускорения точки, второй закон Ньютона принимает вид:

Считается, что это «вторая самая известная формула в физике», хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде. Впервые данную форму закона можно встретить в трудах К.Маклорена и Л.Эйлера.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, то и сила инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратное утверждение, т.е установление факта такого движения, не свидетельствует об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю. На этом основано измерение величины силы, когда она компенсируется силой, величина которой известна .

Второй закон Ньютона позволяет измерять величину силы. Например, знание массы планеты и ее центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующую на эту планету со стороны Солнца.

Третий закон Ньютона

Для любых двух тел (назовем их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2, сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2.^[11] Математически закон записывается так:

Этот закон означает, что силы всегда возникают парами «действие-противодействие».^[9] Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел равна нулю:

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть той, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остается в состоянии покоя или равномерного прямолинейного движения. Однако в том случае, если внешние силы подействуют на систему, то ее центр масс начнет двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы.^[3]

Фундаментальные взаимодействия

Все силы в природе основаны на четырех типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные − между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.

Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется берущей из античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».

Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящими через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово сила, заменяя его словом взаимодействие.^[12]

Каждый вид взаимодействия обусловлен обменом соответствующих переносчиков взаимодействия: гравитационное − обменом гравитонов (существование не подтверждено экспериментально), электромагнитное − виртуальных фотонов, слабое − векторных бозонов, сильное − глюонов (и на больших расстояниях — мезонов). В настоящее время электромагнитное и слабое взаимодействия объединены в более фундаментальное электрослабое взаимодействие. Делаются попытки объединения всех четырех фундаментальных взаимодействие в одно (так называемая теория великого объединения).

Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к этим четырем фундаментальным взаимодействиям. Например, трение − это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули,^[13] который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решетки вещества удерживаться около положения равновесия.^[3].

Однако на практике оказывается не только нецелесообразной, но и просто невозможной по условиям задачи подобная детализация рассмотрения вопроса о действии сил.

Гравитация

Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Исааком Ньютоном в его труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчете, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел^[14]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой , прямо пропорциональной произведению масс ( и ) и обратно пропорциональной квадрату расстояния между ними:

Здесь − гравитационная постоянная^[15], значение которой впервые получил в своих опытах Генри Кавендиш. Используя данный закон, можно получить формулы для расчета силы тяготения тел произвольной формы. Теория тяготения Ньютона хорошо описывает движение планет Солнечной системы и многих других небесных тел. Однако, в ее основе лежит концепция дальнодействия, противоречащая теории относительности. Поэтому классическая теория тяготения неприменима для описания движения тел, перемещающихся со скоростью, близкой к скорости света, гравитационных полей чрезвычайно массивных объектов (например, черных дыр), а также переменных полей тяготения, создаваемых движущимися телами, на больших расстояниях от них^[16].

Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривленным траекториям в трехмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырехмерном пространстве-времени, в котором время в разных точках течет по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе^[3].

Электромагнитное взаимодействие

Электростатическое поле (поле неподвижных зарядов)

Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью C. Однако, исходя из требований практики, в качестве основной единицы измерения стали использовать не единицу заряда, а единицу силы электрического тока. Так, в системе СИ основной единицей является ампер, а единица заряда — кулон — производная от него.

Поскольку заряд, как таковой, не существует независимо от несущего его тела, то электрическое взаимодействие тел проявляется в виде той же рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух точечных зарядов величинами и , располагающихся в вакууме, используется закон Кулона. В форме, соответствующей системе СИ, он имеет вид:

где  — сила, с которой заряд 1 действует на заряд 2,  — вектор, направленный от заряда 1 к заряду 2 и по модулю равный расстоянию между зарядами, а  — электрическая постоянная, равная ≈ 8,854187817•10⁻¹²Ф/м. При помещении зарядов в однородную и изотропную среду сила взаимодействия уменьшается в ε раз, где ε — относительная диэлектрическая проницаемость среды.

Сила направлена вдоль линии, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым бы перемещалась лишённая массы заряженная частица. Эти линии начинаются на одном и заканчиваются на другом заряде.

Электромагнитное поле (поле постоянных токов)

Существование магнитного поля признавалось ещё в средние века китайцами, использовавшим «любящий камень» — магнит, в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.

Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.

Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.

Ампер высказал гипотезу, признаваемую в физике, как модель процесса возникновения магнитного поля, заключающуюся в существовании в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.

Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции, лежащим в плоскости, расположенной перпендикулярно по отношению к направлению движения заряда.

Единицей измерения магнитной индукции является тесла: 1 Тл = 1 Т кг с⁻² А⁻²
Количественно задача была решена Ампером, измерявшим силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.

Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга описывается законом Кулона. Однако заряды, находящиеся в движении относительно друг друга создают магнитные поля, посредством которых созданные движением зарядов токов в общем случае приходят в состояние силового взаимодействия.

Принципиальным отличием силы, возникающей при относительном движении зарядов от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сил взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.

В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обоих токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.

Закон взаимодействия токов используется для эталонирования постоянного электрического тока.

Сильное взаимодействие

Сильное взаимодействие — короткодействующие силы между адронами и кварками. В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающее отталкивание, благодаря этому атомные ядра не «схлопываютс­я­».

Внутри самих адронов сильное взаимодействие удерживает вместе кварки — составные части адронов. Квантами сильного поля являются глюоны. Каждый кварк имеет один из трёх «цветовых» зарядов, каждый глюон состоит из пары «цвет»-«антицвет». Глюоны связывают кварки в т. н. «конфайнмент», из-за которого на данный момент свободные кварки в эксперименте не наблюдались. При отдалении кварков друг от друга энергия глюонных связей возрастает, а не уменьшается как при ядерном взаимодействии. Затратив много энергии (столкнув адроны в ускорителе) можно разорвать кварк-глюонную связь, но при этом происходит выброс струи новых адронов. Впрочем, свободные кварки могут существовать в космосе: если какому-то кварку удалось избежать конфайнмента во время Большого взрыва, то вероятность аннигилировать с соответствующим антикварком или превратиться в бесцветный адрон для такого кварка исчезающе мала.

Слабое взаимодействие

Слабое взаимодействие — фундаментальное короткодействующее взаимодействие. Радиус действия 10⁻¹⁸ м. Симметрично относительно комбинации пространственной инверсии и зарядового сопряжения. В слабом взаимодействии участвуют все фундаментальные фермионы (лептоны и кварки). Это единственное взаимодействие, в котором участвуют нейтрино (не считая гравитации, пренебрежимо малой в лабораторных условиях), чем объясняется колоссальная проникающая способность этих частиц. Слабое взаимодействие позволяет лептонам, кваркам и их античастицам обмениваться энергией, массой, электрическим зарядом и квантовыми числами — то есть превращаться друг в друга. Одно из проявлений — бета-распад.

Производные виды сил

Данные виды сил носят феноменологический характер и определяются с помощью теории определяющих соотношений.

Сила упругости — сила упругого сопротивления тела внешней нагрузке. Является макроскопической реакцией межмолекулярного электромагнитного взаимодействия материала тела. Снижается при появлении нарушений микроструктуры тела — при появлении остаточной деформации тела. Направлена против внешней силы.

Сила трения — сила сопротивления относительному перемещению контактирующих поверхностей тел. Зависит от шероховатости и электромагнитной природы материалов контактирующих поверхностей. Сила трения чистых «зеркальных» поверхностей является макроскопическим проявлением их межмолекулярного взаимодействия. Вектор силы трения направлен противоположно вектору относительной скорости.

Сила сопротивления среды — сила, возникающая при движении твёрдого тела в жидкой или газообразной среде. Относится к диссипативным силам. Сила сопротивления имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Вектор силы сопротивления направлен противоположно вектору скорости.

Сила нормальной реакции опоры — упругая сила, действующая со стороны опоры и противодействующая внешней нагрузке.

Силы поверхностного натяжения — силы, возникающие на поверхности фазового раздела. Имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. Сила натяжения направлена по касательной к поверхности раздела фаз; возникает вследствие нескомпенсированного притяжения молекул, находящихся на границе раздела фаз, молекулами, находящимися не на границе раздела фаз.

Осмотическое давление

Силы Ван-дер-Ваальса — электромагнитные межмолекулярные силы, возникающие при поляризации молекул и образовании диполей. Ван-дер-Ваальсовы силы быстро убывают с увеличением расстояния.

Сила инерции

Сила инерции — фиктивная сила, вводимая в неинерциальных системах отсчёта. Введение сил инерции производится для того, чтобы придать уравнениям движения тел в неинерциальных системах отсчёта ту же форму, какую имеет уравнение второго закона Ньютона в инерциальных системах. В ряде случаев такой подход позволяет сделать рассмотрение движения более удобным и наглядным, а решение соответствующих задач — более простым.

В частности, в системе отсчёта, связанной с равноускоренно движущимся телом, сила инерции направлена противоположно ускорению. Из полной силы инерции, представляющей собой сумму переносной и кориолисовой, могут быть для удобства выделены центробежная сила и сила Кориолиса.

Силы инерции принципиально отличаются от всех остальных сил тем, что никакому реальному взаимодействию тел они не соответствуют.

Равнодействующая сила

При расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей. Это геометрическая сумма всех сил, действующих на тело. При этом действие каждой силы не зависит от действия других, то есть каждая сила сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил (принцип суперпозиции).

См. также

Источники

Примечания

1. ↑ Glossary. Earth Observatory. NASA. — «Сила — любой внешний фактор, который вызывает изменение в движении свободного тела или возникновение внутренних напряжений в зафиксированном теле.»  (англ.)
2. ↑ Бронштейн И. Н. Семендяев К. А. Справочник по математике. М.: Издательство «Наука» Редакция справочной физико-математической литературы.1964.
3. ↑ ^{1 2 3 4 5} Feynman, R. P., Leighton, R. B., Sands, M. Lectures on Physics, Vol 1. — Addison-Wesley, 1963.  (англ.)
4. ↑ Kleppner, D., Kolenkow, R. J. An introduction to mechanics. — McGraw-Hill.  (англ.)
5. ↑ ^{1 2 3} University Physics, Sears, Young & Zemansky, pp. 18-38  (англ.)
6. ↑ Хайкин С. Э.Силы инерции и невесомость. Изд-во «Наука» М.,1967, с илл.
7. ↑ Weinberg, S. Dreams of a Final Theory. — Vintage Books USA, 1994. — ISBN 0-679-74408-8  (англ.)
8. ↑ Heath,T.L. The Works of Archimedes (1897). Archive.org. Архивировано из первоисточника 23 августа 2011. Проверено 14 октября 2007.  (англ.)
9. ↑ ^{1 2 3 4} Newton, I. The Principia Mathematical Principles of Natural Philosophy. — University of California Press, 1999. — ISBN 0-520-08817-4  (англ.)
10. ↑ Мултановский В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 80−81.
11. ↑ Henderson, Tom Lesson 4: Newton’s Third Law of Motion. The Physics Classroom (1996-2007). Архивировано из первоисточника 23 августа 2011. Проверено 4 января 2008.  (англ.)
12. ↑ Капра, Фритьоф ДАО ФИЗИКИ. СПб.,»ОРИС»*»ЯНА-ПРИНТ». 1994 г. 304 с. ISBN 5-88436-021-5
13. ↑ Nave, R Pauli Exclusion Principle. HyperPhysics***** Quantum Physics. Архивировано из первоисточника 23 августа 2011. Проверено 2 января 2008.  (англ.)
14. ↑ University Physics, Sears, Young & Zemansky, pp. 59−82  (англ.)
15. ↑ Sir Isaac Newton: The Universal Law of Gravitation. Astronomy 161 The Solar System. Архивировано из первоисточника 23 августа 2011. Проверено 4 января 2008.  (англ.)
16. ↑ «Тяготение». Новиков И. Д. // Физическая энциклопедия. Гл. ред. Прохоров А. М. — М.: «Большая Российская энциклопедия», 1998. — Т. 5. — С. 188−193. — 760 с. — ISBN 5-85270-101-7

Сила (значения) — Википедия

Материал из Википедии — свободной энциклопедии

Сила — в наиболее привычном повседневном употреблении: механическое воздействие на что-либо, без конкретизации. В разных областях знания имеет различные значения.

• Физические термины со словом «сила», несущие иной смысл:

• Военная сила — вся совокупность средств вооружённого принуждения, которые доступны каким-либо субъектам международной политики.
• Вооружённые силы — армия, авиация и флот какого-либо государства. См. также силы (силы обороны, самообороны, сторон и т.п.) различных государств.
• Жёсткая сила — форма внешнеполитической стратегии, подразумевающая принуждение.
• Живая сила — часть воинского подразделения, состоящая из людей и животных.
• Жизненная сила — по философской теории витализма: некая сверхъестественная сила в живых существах.
• Мягкая сила — форма стратегии, основанная на акцентуации привлекательности собственной позиции.
• Производительные силы — средства производства и люди, приводящие их в действие.
• Рабочая сила — в политэкономии: способность человека к труду, число готовых работать по найму людей.
• Сила — насильственное принуждение к выполнению требований.
• Сила (также социальная сила, общественная сила, политическая сила) — группа людей, влияющих на общественные события, либо способности этой группы на них влиять.
• Сила Божия (благодать) — в христианском богословии: нетварная Божественная сила или энергия, в которой Бог являет Себя человеку и которая даруется человеку для его спасения.
• Сила роста — в экономике: процентная ставка, цена денег как средства сбережения.
• Силы — в богословии: ангельский чин второго лика.
• Силы Портера — в экономике: подлежащие анализу пять сил-угроз: появление продуктов-заменителей, новые игроки, власть поставщиков, власть потребителей, уровень конкурентной борьбы.
• Юридическая сила — применимость закона.

• Сила — мужское имя; известные носители:
  • Сила — апостол от семидесяти, сподвижник апостола Павла, жил в I веке.
  • Сила — митрополит, епископ Константинопольской православной церкви, жил в XX веке.
  • Гагарин, Сила Иванович — сын боярский, письменный голова, воевода.
  • Мищенко, Сила Моисеевич — советский военачальник, участник Первой мировой и Гражданской войн.
  • Сандунов, Сила Николаевич — российский актер и предприниматель.
• Сила — женское имя; известные носители:
  • Сахин, Сила — немецкая актриса турецкого происхождения.
  • Уорд, Сила — американская актриса, лауреат двух премий «Эмми» и «Золотого глобуса».
• Сила-Новицкий — польская фамилия; известные носители:

• В музыкальных произведениях и изданиях:
  • «Сила» — альбом группы ТНМК, выпущенный в 2005 году.
  • «Сила сопротивления» — совместный проект (2010) двух коллективов из Омска.
  • «Сила судьбы» — опера Джузеппе Верди.
  • «Сила трёх» — студийный альбом российской поп-группы Serebro (2016).
  • «Сила ума» — альбом (2002), смесь рэпа, хардкора, рэпкора и нью-метала.
• В литературных произведениях:
  • «Сила есть право» — книга (1896) об идеях социального дарвинизма.
  • «Сила и материя» — книга (1855) немецкого вульгарного материалиста Л. Бюхнера.
  • «Сила и слава» — роман Грэма Грина, признанный классикой мировой литературы.
  • «Сила каббалы» — популярное изложение каббалы в трактовке «Центра изучения Каббалы».
  • «Сила шести» — научно-фантастический роман Джеймса Фрея и Джоби Хьюза.
• В кинофильмах и телефильмах:
  • «Сила веры» — американский кинофильм (1992), трагикомедия.
  • «Сила внутри нас» — немой художественный фильм Петра Чардынина (1915).
  • «Сила воли» — фильм-драма об афро-американском спортсмене Джесси Оуэнсе.
  • «Сила зла» — фильм режиссёра Абрахама Полонски.
  • «Сила зла — фильм ужасов режиссёра Эвана Ли.
  • «Сила Кролла» — серия британского научно-фантастического телесериала «Доктор Кто».
  • «Сила личности» — кинофильм, драма режиссёра Джона Эвилдсена.
  • «Сила любви» — американский немой фильм 1922 года.
  • «Сила любви» — американский фильм 1980 года.
  • «Сила любви»^[1] — индийский фильм 1983 года.
  • «Сила Магнума» — художественный фильм, второй в серии фильмов о Грязном Гарри.
  • «Сила ниндзя» — фильм (1984) режиссёра Wu Kuo-Jen.
  • «Сила огня» — кинофильм.
  • «Сила страсти» — кинофильм, экранизация произведения принца Михаила Греческого.
  • «Силы природы» — романтическая комедия 1999 года.
  • «Силы» — американская телевизионная адаптация одноимённой серии комиксов.
• В фольклоре:
  • Нечистая сила — собирательное имя потусторонней силы и существ: злых духов, чертей, демонов, водяных, оборотней, нежити и так далее.
  • Сила (Звёздные войны) (Force) — в фантастической вселенной Звёздных войн — свойство живой материи, якобы создаваемое всеми живыми существами, которое окружает и проникает во всё живое и объединяет Галактику.
  • Сила (карта Таро) — карта № 11 старших арканов колоды Таро.
  • Суперсила — обозначение паранормальных способностей вымышленных героев.

СИЛА — это… Что такое СИЛА?

СИ́ЛА

силы, ж.

1. Способность живых существ производить физические действие, энергия, порождаемая способностью управлять движениями мышц. «Какой-то муравей был силы непомерной…» Крылов. «Пригожеством, ростом и силой ты ровни в селе не имел.» Некрасов. «Силы коняге набраться неоткуда.» Салтыков-Щедрин. «Санька… захлопнула дверь изо всей силы.» А.Н.Толстой. Обладать огромной силой. Ударить с силой.

|| только ед. Физическое воздействие, насилие. «Смекнул старик, что тут силой не возьмешь.» Салтыков-Щедрин. Действовать убеждением, а не силой. Применять силу.

|| только мн. Жизнедеятельность, физическая энергия, бодрость. Выбиться из сил (см. выбиться). Собраться с силами (см. собраться). Лишиться сил. Приняться за работу со свежими силами. В расцвете сил.

2. Напряжение, энергия как причина, выводящая тело, материю из состояния покоя или изменяющая направление, скорость движения (науч.). Центробежная сила. Сила тяжести. Равнодействующая сила. Сила инерции. Сила притяжения земли. Сила натяжения нити.

|| только ед. Интенсивность, напряженность чего-н., степень напряжения; в механике – величина, равная произведению массы тела на его ускорение. Сила света. Сила звука. Сила взрыва. Сила ветра. Сила тока. В физике за единицу силы принята дина. Сила, с к-рой вылетает пробка.

|| только мн. Материя, все материальное как источник деятельности, движения, изменений. Производительные силы (см. производительный). «В Советском Союзе идет возрождение многочисленных национальностей, идет подъем хозяйственных сил и национальных культур всех народов.» Молотов. «Наш опыт, опыт строителей коммунистического общества, уже полностью показал, что возможности роста сил СССР неограниченно велики.» Молотов. Использование водных сил страны.

3. Способность проявления какой-н. деятельности, характерная степенью, устремленностью, напряженностью проявления этой деятельности. Сила воли. Сила ума. Сила привычки. Сила фантазии. Сила таланта. Талант огромной силы. «Плохо верится в силу добра.» Некрасов. «Человеку прекрасней и шире можно силы свои развернуть.» Некрасов. Душевные силы.

|| только мн. Средство, способ проявления деятельности. «Он всеми силами старался свергнуть с себя бремя этих упреков.» Гончаров. «Верю всеми силами души – и посвящу этому делу всю свою жизнь» Тургенев.

4. Вообще – источник чего-н., какой-н. деятельности, явления. «Ты был всегда ареной деятельной силы, пытливой мысли и труда!» Некрасов. «Непреодолимая сила влекла меня к ней.» Тургенев. Советская молодежь – великая творческая сила.

5. только ед. Влияние, авторитет, власть, могущество. …«Сила современного движения – пробуждение масс…» Ленин. «Сила пролетариата в любой капиталистической стране несравненно больше, чем доля пролетариата в общей сумме населения.» Ленин. «В подъеме материального положения и культурного развития народных масс сказалась сила, мощь, непобедимость нашей советской революции.» История ВКП(б). Сила печатного слова велика. Он имеет силу в обществе.

6. только ед. Сущность, смысл, значение, роль чего-н. (разг.). Вся сила этого постановления в совершенно новой постановке вопроса. «Не в шитье была там сила.» Некрасов. «Не в том сила, что кобыла сива, а в том, что не везет.» Поговорка.

7. только ед. Правомочность, значение. Старые законы потеряли силу. Приговор вошел в силу. Получить силу закона. Новый закон вступил в силу.

8. только мн. (ед. устар.). Войска, то же, что вооруженные или военные силы. Двинуть большие силы на противника. Бросить в атаку свежие силы. Главные силы (основная часть войсковой колонны, группы войск). Морские силы. Воздушные силы. Окружить врага несметной силой.

9. преимущ. мн. Общественная группа, слой, характерный какими-н. отличительными признаками. «За истекшие годы совершенно изменилось соотношение классовых сил в СССР: создана была новая социалистическая индустрия, разгромлено кулачество, победил колхозный строй…» История ВКП(б). – «Для кого мало наших открытых предупреждений, тот узнает об этом в свое, ему положенное время. И тем победоноснее, тем значительнее в международном смысле будут наши успехи в этой грядущей борьбе с силами внешней агрессии, чем больше и чем плодотворнее мы поработаем над коммунистическим воспитанием в нашей стране.» Молотов. «С развитием капитализма в России рабочий класс становился могучей передовой силой, способной к организованной революционной борьбе.» История ВКП(б). Революционные силы. Живые силы страны.

10. только ед. Огромное количество (простореч.). «Лука этакой силы денег дать и сообразить не мог.» Лесков. «Ныне сила хлеба.» Даль.

11. Тв. п. мн. ч. силами употр. также в знач. при помощи кого-чего-н. Спектакль поставлен силами местных артистов. Устроить концерт своими силами. Собственными силами. Силами коллектива. ❖ Взять силу (простореч.) – усилиться, окрепнуть. «Огонь силу взял.» Даль. Военная сила – о действиях войск. Применить военную силу. Военные или вооруженные силы – армия, войска. Вооруженные силы страны. Войти в силу – 1) то же, что взять силу. «Конопляники уже вошли в силу и пускают свой тяжелый, но приятный дух.» Тургенев. 2) перен. стать влиятельным, авторитетным. В силах – 1) без доп. и с инф. с неослабевшими силами, в состоянии что-н. делать (по своему здоровью). «Пока я в силах, поработаю. Я не в силах сносить этой пытки.» Гончаров. 2) с инф. иметь возможность, власть (чаще с отрицанием). «И то, что в жизни взято раз, не в силах рок отнять у нас.» Некрасов. «Только содержащий все общество класс пролетариев в силах произвести социальную революцию.» Ленин. В силе – 1) в таком состоянии, когда есть власть, влияние. «Колхозы и совхозы были слабы, а кулак был еще в силе.» Сталин.(о 1924 г.). 2) в полном развитии, в разгаре (простореч.). «Игра уж в самой силе.» Лермонтов. В силу (устар.) – то же, что под силу. «Куме совсем не в силу труд.» Крылов. В силу чего (или, реже, всилу; книжн.) – вследствие, по причине. В силу создавшихся условий. Лошадиная сила – см. лошадиный. Нечистая сила – см. нечистый. От силы (простореч.) – самое бо́льшее, самое вероятное. Ему от силы 20 лет. Здесь от силы два кило. По мере сил – см. мера. По силам или по силе – соответственно возможностям, силам, способностям. По силе возможности (простореч.) – то же, что по мере возможности (см. мера). Под силу – соответствует силам, возможностям, в состоянии справиться с чем-н. «Мне не под силу, брат, я чувствую, что глуп.» Грибоедов. «Современному французскому буржуа ни героизм, ни идеалы уже не под силу.» Салтыков-Щедрин. Рабочая сила – см. рабочий (2). Сил нет – 1) отсутствуют силы делать что-н., нет возможности справиться (см. сила в 1 знач.). «Сил нам нет кружиться доле.» Пушкин. «От напора ветра нет сил дышать.» Чехов. 2) перен. употр. при выражении отчаяния, бессилия что-н. сделать, чем-н. воспрепятствовать чему-н. (разг. фам.). Сил нет, как надоел своей болтовней. Силою в (от, до; воен.) – количеством, численностью. Колонна силою в тысячу штыков. Колонна силою около полка. Силою вещей (книжн.) – по причине сложившихся обстоятельств, условий. Капитализм силою вещей обречен на гибель. Силы небесные (церк., устар.) – первонач. ангелы как небесное воинство, а позднее вообще – мистические силы неба, божества. С нами крестная сила – см. крестный. Через силу – сверх имеющихся возможностей, сил, способностей. Что есть силы или что было силы (или сил; разг.) – изо всех сил. «Комар, что было сил, сонливца укусил.» Крылов. «Что силы есть, хвать друга камнем в лоб.» Крылов.

Толковый словарь Ушакова. Д.Н. Ушаков. 1935-1940.

Единицы силы. Динамометр. Видеоурок. Физика 7 Класс

Тема: Взаимодействие тел

Урок: Единицы силы. Динамометр

Прежде всего, вспомним, что такое сила. Когда на тело действует другое тело, физики говорят, что со стороны другого тела на данное тело действует сила.

Сила – это физическая величина, характеризующая действие одного тела на другое.

Сила обозначается латинской буквой F, а единица силы в честь английского физика Исаака Ньютона называется ньютоном (пишем с маленькой буквы!) и обозначается Н (пишем заглавную букву, так как единица названа в честь ученого). Итак,

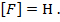
Наравне с ньютоном, используются кратные и дольные единицы силы:

килоньютон 1 кН = 1000 Н;

меганьютон 1 МН = 1000000 Н;

миллиньютон 1 мН = 0,001 Н;

микроньютон 1 мкН = 0,000001 Н и т. д.

Под действием силы скорость тела изменяется. Другими словами, тело начинает двигаться не равномерно, а ускоренно. Точнее, равноускоренно: за равные промежутки времени скорость тела меняется одинаково. Именно изменение скорости тела под действием силы физики используют для определения единицы силы в 1 Н.

Единицы измерения новых физических величин выражают через так называемые основные единицы – единицы массы, длины, времени. В системе СИ – это килограмм, метр и секунда.

Пусть под действием некоторой силы скорость тела массой 1 кг изменяет свою скорость на 1 м/с за каждую секунду. Именно такая сила и принимается за 1 ньютон.

Один ньютон (1 Н) – это сила, под действием которой тело массой 1 кг изменяет свою скорость на 1 м/с каждую секунду.

Экспериментально установлено, что сила тяжести, действующая вблизи поверхности Земли на тело массой 102 г, равна 1 Н. Масса 102 г составляет приблизительно 1/10 кг, или, если быть более точным,

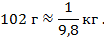
Но это означает, что на тело массой 1 кг, то есть на тело в 9,8 раз большей массы, у поверхности Земли будет действовать сила тяжести 9,8 Н. Таким образом, чтобы найти силу тяжести, действующую на тело любой массы, нужно значение массы (в кг) умножить на коэффициент, который принято обозначать буквой g:

Мы видим, что этот коэффициент численно равен силе тяжести, которая действует на тело массой 1 кг. Он носит название ускорение свободного падения. Происхождение названия тесно связано с определением силы в 1 ньютон. Ведь если на тело массой 1 кг действует сила не 1 Н, а 9,8 Н, то под действием этой силы тело будет изменять свою скорость (ускоряться) не на 1 м/с, а на 9,8 м/с каждую секунду. В старшей школе этот вопрос будет рассмотрен более подробно.

Теперь можно записать формулу, позволяющую рассчитать силу тяжести, действующую на тело произвольной массы m(Рис. 1).

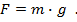
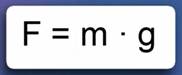
Рис. 1. Формула для расчета силы тяжести

Следует знать, что ускорение свободного падения равно 9,8 Н/кг только у поверхности Земли и с высотой уменьшается. Например, на высоте 6400 км над Землей оно меньше в 4 раза. Однако при решении задач этой зависимостью мы будем пренебрегать. Кроме того, на Луне и других небесных телах также действует сила тяжести, и на каждом небесном теле ускорение свободного падения имеет свое значение.

На практике часто приходится измерять силу. Для этого используется устройство, которое называется динамометр. Основой динамометра является пружина, к которой прикладывают измеряемую силу. Каждый динамометр, помимо пружины, имеет шкалу, на которую нанесены значения силы. Один из концов пружины снабжен стрелкой, которая указывает на шкале, какая сила приложена к динамометру (Рис. 2).

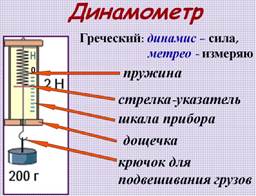
Рис. 2. Устройство динамометра

В зависимости от упругих свойств пружины, использованной в динамометре (от ее жесткости), под действием одной и той же силы пружина может удлиняться больше или меньше. Это позволяет изготавливать динамометры с различными пределами измерения (Рис. 3).

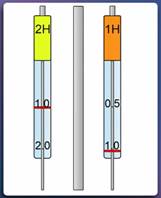
Рис. 3. Динамометры с пределами измерения 2 Н и 1 Н

Существуют динамометры с пределом измерения в несколько килоньютонов и больше. В них используется пружина с очень большой жесткостью (Рис. 4).

Рис. 4. Динамометр с пределом измерения 2 кН

Если подвесить к динамометру груз, то по показаниям динамометра можно определить массу груза. Например, если динамометр с подвешенным к нему грузом показывает силу 1 Н, значит, масса груза равна 102 г.

Обратим внимание на то, что сила имеет не только численное значение, но и направление. Такие величины называют векторными. Например, скорость – это векторная величина. Сила – также векторная величина (говорят еще, что сила – вектор).

Рассмотрим следующий пример:

Тело массой 2 кг подвешено на пружине. Необходимо изобразить силу тяжести, с которой Земля притягивает это тело, и вес тела.

Вспомним, что сила тяжести действует на тело, а вес – это сила, с которой тело действует на подвес. Если подвес неподвижен, то численное значение и направление веса такие же, как у силы тяжести. Вес, как и сила тяжести, рассчитываются по формуле, изображенной на рис. 1. Массу 2 кг необходимо умножить на ускорение свободного падения 9,8 Н/кг. При не слишком точных расчетах часто ускорение свободного падения принимают равным 10 Н/кг. Тогда сила тяжести и вес приблизительно будут равны 20 Н.

Для изображения векторов силы тяжести и веса на рисунке необходимо выбрать и показать на рисунке масштаб в виде отрезка, соответствующего определенному значению силы (например, 10 Н).

Тело на рисунке изобразим в виде шара. Точка приложения силы тяжести – центр этого шара. Силу изобразим в виде стрелки, начало которой расположено в точке приложения силы. Стрелку направим вертикально вниз, так как сила тяжести направлена к центру Земли. Длина стрелки, в соответствии с выбранным масштабом, равна двум отрезкам. Рядом со стрелкой изображаем букву 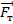, которой обозначается сила тяжести. Так как на чертеже мы указали направление силы, то над буквой ставится маленькая стрелка, чтобы подчеркнуть, что мы изображаем векторную величину.

Поскольку вес тела приложен к подвесу, начало стрелки, изображающей вес, помещаем в нижней части подвеса. При изображении также соблюдаем масштаб. Рядом помещаем букву 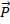, обозначающую вес, не забывая над буквой поместить небольшую стрелку.

Полное решение задачи будет выглядеть так (Рис. 5).

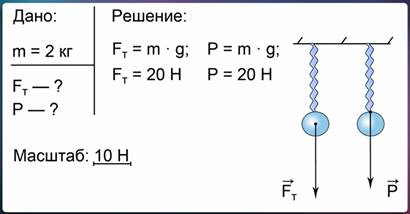
Рис. 5. Оформленное решение задачи

Еще раз обратите внимание на то, что в рассмотренной выше задаче численные значения и направления силы тяжести и веса оказались одинаковыми, а точки приложения – различными.

При расчете и изображении любой силы необходимо учитывать три фактора:

· численное значение (модуль) силы;

· направление силы;

· точку приложения силы.

Сила – физическая величина, описывающая действие одного тела на другое. Обычно она обозначается буквой F. Единица измерения силы – ньютон. Для того чтобы рассчитать значение силы тяжести, необходимо знать ускорение свободного падения, которое у поверхности Земли составляет 9,8 Н/кг. С такой силой Земля притягивает к себе тело массой 1 кг. При изображении силы необходимо учитывать ее числовое значение, направление и точку приложения.

 

Список литературы

1. Перышкин А. В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
2. Перышкин А. В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
3. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

 

Дополнительные ссылки на ресурсы сети Интернет

1. Единая коллекция цифровых образовательных ресурсов (Источник).
2. Единая коллекция цифровых образовательных ресурсов (Источник).
3. Единая коллекция цифровых образовательных ресурсов (Источник).
4. Единая коллекция цифровых образовательных ресурсов (Источник).

 

Домашнее задание

1. Лукашик В. И., Иванова Е. В. Сборник задач по физике для 7–9 классов №327, 335–338, 351.

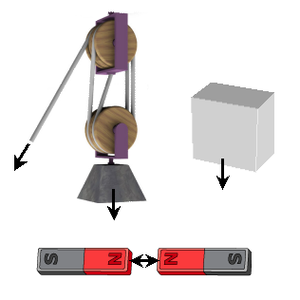
Виды сил. Видеоурок. Физика 7 Класс

Тела взаимодействуют, и эти взаимодействия влияют на то, будет ли двигаться тело и как именно. Силы взаимодействия определяют ускорение. Какова природа этих сил? Можно толкнуть тело рукой, и оно сдвинется – с таким действием всё понятно. Но есть множество других взаимодействий. Например, если мы разожмём пальцы, то тело упадёт вниз. В воздухе тело упадет быстрее, чем тонуло бы в воде. Это означает, что на тело действуют какие-то силы. Тело лежит на столе и давит на него – тоже взаимодействие. Вещества состоят из структурных частиц – эти частицы как-то взаимодействуют друг с другом. Возникает вопрос, как это всё учесть и рассчитать, ведь нам приходится отвечать на вопрос: «Что, если…?», предсказывать явления.

Любые два тела притягиваются. Явление притяжения по-другому называют гравитацией. Мы её ощущаем по тому, что Земля притягивает тела: преодолеваем гравитацию, когда поднимаем что-то тяжелое, и наблюдаем её действие, когда тело падает. Сила притяжения зависит от масс тел и от расстояния между ними. Масса Земли огромна, поэтому к ней тела притягиваются заметно. Две книги на полке тоже притягиваются друг к другу, но так слабо из-за малых масс, что мы этого не замечаем.

Притягивает ли нас Луна? А Солнце? Да, но намного меньше, чем Земля, из-за большого расстояния. Мы на себе притяжение Луны не ощущаем, а вот приливы и отливы происходят из-за притяжения Луны и Солнца. А черные дыры обладают настолько большой массой, что притягивают даже свет: проходящие мимо лучи искривляются.

Все тела притягиваются. Возьмем тело, которое лежит на столе. Оно притягивается к Земле, но остается на месте. Чтобы сохранялось состояние покоя, силы, действующие на тело, должны быть уравновешены. Значит должна быть сила, которая уравновешивает силу тяжести. В данном случае это сила, с которой на тело действует стол. Такую силу назвали силой реакции опоры (см. рис. 1).

При этом тело давит на стол. Если мы рассматриваем, как движется тело, нам не важно, что происходит со столом. Но если мы рассматриваем, что произойдет со столом, то нужно будет учесть это воздействие. Силу, с которой тело действует на опору или подвес, назвали весом:

Рис. 1. Взаимодействие гири и стола

Чтобы сдвинуть любое тело, надо приложить силу. В этом и заключается инертность. Если мы попробуем сдвинуть гирю на столе, она до некоторого предела вообще не сдвинется. Значит и здесь возникает некоторая сила, которая уравновешивает наше воздействие. Эта сила – сила трения:

Рис. 2. Сила трения

 Что-то похожее происходит, когда мы поднимаем гирю. Она тоже сначала не поднимается, пока наша сила не превзойдет порог: здесь этот порог – сила притяжения Земли.

Если вместо стола будет пружина, она сожмется, и будет также действовать на это тело. Тело действует на стол или пружину, они прогибаются, их молекулы смещаются (см. рис. 3), а при смещении молекул между ними возникают силы отталкивания, препятствующие дальнейшей деформации:

Рис. 3. Сила отталкивания

Отличие в том, что деформация стола чаще всего настолько мала, что ее трудно заметить, а некоторые тела деформируются значительно больше, как пружина или резинка. Мало того, по деформации такого тела можно судить о силе, которая в нем возникла. Это удобно для расчетов, поэтому эту силу изучают отдельно – ее назвали силой упругости.

А если тело положить на поверхность воды? В воде многие предметы становятся легче, значит, есть сила, которая их «приподнимает». Для некоторых тел ее достаточно, чтобы они плавали на поверхности – это и кусок пенопласта или древесины, и корабль. Благодаря этой силе мы вообще можем плавать. Эту силу назвали силой Архимеда.

Конечно, эта классификация достаточно условна. Природа силы реакции опоры и силы упругости одна и та же, но удобно их изучать отдельно. Или рассмотрим такой случай: гиря лежит на опоре и ее тянут вверх за нитку. Гиря действует и на опору, и на нитку – какую из этих сил считать весом и как назвать вторую силу? Важно рассмотреть две силы, на что они действуют, и решать задачу независимо от названий. По большому счету есть только взаимодействие атомов, но для удобства мы придумали несколько моделей.

Можно провести опыт: подвесить на нити два груза на перекладине, чтобы они уравновесились. Если мы поднесём к одному из грузов гирю, система будет вращаться, это значит, что грузик и гиря притягиваются друг к другу. Действует закон всемирного тяготения.

---

 

Закон всемирного тяготения

Исаак Ньютон сформулировал закон всемирного тяготения:

Любые два тела притягиваются друг к другу, причем сила притяжения прямо пропорциональна массам этих тел, и обратно пропорциональна расстоянию между их центрами масс. Математически закон всемирного тяготения записывается так:

где m_(1,2) – массы взаимодействующих тел, а R — расстояние между их центрами масс. Силы всемирного тяготения также называют гравитационными силами, а коэффициент пропорциональности G в законе всемирного тяготения называют гравитационной постоянной. Она равна .

Закон всемирного тяготения можно использовать для вычисления сил притяжения между любыми телами. Представьте, вы сидите перед монитором. Допустим, масса монитора равна 2 кг, а масса человека – 70 кг, расстояние примем равным 1 м. Тогда сила взаимодействия по формуле получится есть 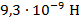. Это настолько мало, что мы абсолютно не замечаем такое слабое взаимодействие. Коэффициент пропорциональности G в формуле принимает очень малое значение, 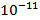. Если на земле будет лежать гвоздь и мы поднесем к нему магнит, то гвоздь притянется к маленькому магниту сильнее, чем к планете. Тем не менее, если взять взаимодействие двух небесных тел, например, планет, то в формулу надо будет подставлять огромные массы, тогда сила будет гораздо больше, несмотря на большие расстояния. Да и на движение небольших тел вблизи поверхности Земли, Земля оказывает значительное влияние.

---

Сила тяжести – это сила, с которой тело притягивается к Земле. Конечно, другие планеты тоже вступают в гравитационное взаимодействие и для них тоже можно вычислить силу тяжести. Гравитационные силы, а значит и сила тяжести, направлены по отрезку, соединяющему центры масс взаимодействующих тел. Мы привыкли направление к центру Земли называть «вниз».

Галилео Галилей опытным путем установил: все тела вблизи поверхности Земли падают с одинаковым ускорением. Рассмотрим случай, когда на тело действует только сила тяжести. Эта сила и дает телу ускорение, по второму закону Ньютона 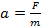. Дело в том, что если увеличить массу тела 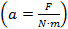, сила тяжести увеличится во столько же раз , и из формулы увидим, что тело будет двигаться с тем же ускорением: 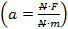 То есть для разгона с тем же ускорением более тяжелых тел нужна бόльшая сила, и на них как раз и действует бόльшая сила тяжести. Это называется ускорением свободного падения. Для Земли оно равно примерно 9,8 м/.

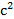Принято обозначать это ускорение буквой «g». Сама же сила тяжести чаще всего обозначается как F_{тяжести}, или кратко F_т. И по ускорению, которое создает сила, можно найти саму силу:

---

 

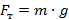
Почему бумага падает медленнее железа?

Мы рассматривали движение тел, на которые действует только сила тяжести. Эта сила сообщает всем телам одинаковое ускорение. Но не всегда действием остальных сил можно пренебречь. Например, при определенной форме тела существенной становится сила сопротивления воздуха. Возьмем железный шарик и скомканный лист бумаги такой же массы. Силы тяжести на них действуют одинаковые, но на бумагу дополнительно действует сопротивление воздуха, которым пренебречь нельзя, и поэтому бумага движется с другим ускорением. Если бросить железо и бумагу в безвоздушном пространстве, то можно снова рассматривать ситуацию, когда на тело действует только сила тяжести, и оба тела упадут с одним и тем же ускорением.

---

Даже если тело лежит на столе, на него действует та же сила тяжести, которую мы так же рассчитываем по формуле: масса на ускорение свободного падения. Казалось бы, при чем здесь ускорение, когда тело не движется? Так вот, это ускорение, с которым тело двигалось бы, если бы на него действовала только сила тяжести. По этому ускорению можно рассчитать силу, она будет той же: .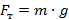

---

 

«Ускорение свободного падения в разных частях Земли»

Принято считать величину “g”, то есть ускорение свободного падения, величиной постоянной, равной около 9,8 м/с². Но с оговоркой: «для нашей планеты». На других небесных телах так же действуют силы тяготения, но ускорение свободного падения там отличаются от нашего. Например, на Марсе ускорение свободного падения всего 3,71 м/с².
Но на самом деле, даже на одной нашей планете это ускорение будет иметь разные значения в разных местах на Земле.

Известное число 9,8 – это усредненное значение для всей планеты. Наша планета, как известно, не круглая, а немного приплюснута на полюсах. И именно на этих полюсах, ускорение свободного падения немного больше, чем на других широтах: на полюсах g = 9,832 м/с², а на экваторе — 9,78 м/с².

Это объясняется тем, что ускорение свободного падения зависит от расстояния до центра Земли.

Формула, по которой можно найти ускорение: 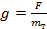 (сила тяжести, действующая на тело, делить на массу этого тела). Сила гравитационного взаимодействия: .  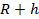— это расстояние от центра Земли до тела, если R – это радиус Земли, а тело находится на высоте h над поверхностью. Разделим силу на массу тела и получим ускорение свободного падения: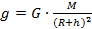

Чем больше расстояние, тем меньше ускорение свободного падения. Поэтому в горах оно меньше, чем у поверхности Земли.

Чем больше расстояние от тела до планеты, тем слабее действует на него сила тяжести и тем меньше ускорение свободного падения. Вблизи поверхности можно считать h равным нулю, тогда g будет постоянным и равным 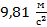. Какую высоту мы еще можем считать «вблизи», а какую уже нет? Точность диктуется целью задачи. Для некоторых задач мы можем считать g постоянным на высотах в сотни километров. Если мы рассматриваем книгу, лежащую на столике в летящем самолете, то нам не так важно, что ускорение свободного падения будет отличаться на несколько сотых 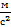. А если мы рассчитываем запуск спутника, нам нужна бόльшая точность, эти несколько сотых  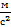нельзя опустить, приходится учитывать даже отличия радиуса Земли на экваторе и на полюсах. Для многих задач, достаточно привычного значения  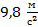или даже .

---

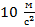Если тело покоится на какой-то поверхности (опоре), то на него действует сила тяжести и сила реакции опоры, и они уравновешиваются.

Сила реакции опоры – это сила, с которой опора действует на тело.

Силы тяжести и реакции опоры приложены к нашему телу и действуют на него. В рассмотренном примере, когда тело лежит на горизонтальной поверхности, сила реакции опоры равна силе тяжести, и направлена в противоположную сторону, то есть вертикально вверх:

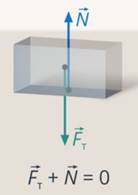
Рис. 4. Сила реакции опоры

Обычно обозначают силу реакции опоры буквой N.

Опора действует на тело, а тело действует на опору (или нить, если оно висит на нити).

Вес тела – это сила, с которой тело действует на опору или подвес:

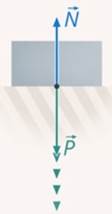
Рис. 5. Вес тела

Вес тела чаще всего обозначают буквой «Р», и по модулю он равен силе реакции опоры (по третьему закону Ньютона: с какой силой одно тело действует на другое, с такой же силой второе тело действует на первое): P=N.

Если тело покоится на горизонтальной поверхности, на него действуют сила тяжести и сила реакции опоры. Они уравновешиваются, 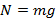. Тогда и вес равен .

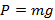Часто понятие «вес тела» путают с массой тела. Это уже стало нормой для разговорной речи: «взвесить», «сколько весишь», «весы». Вес – это сила, с которой тело действует, а масса – характеристика самого тела, мера инертности. Легко проверить: стоя на весах, мы видим значение массы, которое вычислено по весу. Если немного подпрыгнуть, то цифра изменится. Но ведь масса не поменялась. Это поменялся вес, сила, с которой мы давим на поверхность весов. А на МКС космонавт вообще не давит на весы, его вес равен нулю – и это состояние называется невесомость.

Тело тоже притягивает Землю, но на движение огромной Земли эта сила не влияет, поэтому ее не рассматривают. Прикасаясь к опоре, тело давит на опору своим весом, а опора на тело – с силой реакции опоры. Это вторая пара сил в этой системе. Если мы описываем движение конкретного тела, мы рассматриваем силы, которые действуют на него, например, сила тяжести и сила реакции опоры.

Рассмотрим силу, которая возникает, когда одни тела движутся относительно других, соприкасаясь с ними – силу трения.

Сила трения — сила, возникающая в месте соприкосновения тел и препятствующая их перемещению друг относительно друга:

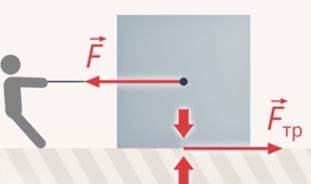
Рис. 6. Сила трения

Если пнуть мяч – он покатится и через какое-то время остановится. Санки, с какой бы высокой горки ни съехали – также остановятся.

Рассмотрим два вида трения. Первое – это когда одно тело скользит по поверхности другого — например, при спуске с горы на санках, его назвали трение скольжения. Второе – когда одно тело катится по поверхности другого, например, мяч по земле, его назвали трение качения.

Обозначают силу трения ,  и вычисляют по формуле:

где N – сила реакции опоры, с которой мы уже познакомились, а µ — это коэффициент трения между данными двумя поверхностями.

Чем сильнее будут прижаты друг к другу тела, тем сила трения будет больше, то есть сила трения пропорциональна силе реакции опоры.

Трение возникает из-за взаимодействия частиц, из которых состоит вещество. Поверхность не может быть идеально гладкой, всегда есть выступы, шероховатости. Выступающие части поверхностей задевают друг друга и препятствуют движению тела. именно поэтому для движения по гладким (полированным) поверхностям требуется прикладывать меньшую силу, чем для движения по шероховатым.

---

 

Всегда ли трение уменьшается при полировке?

Полируя, мы уменьшаем количество и размер неровностей, которые препятствуют относительному движению двух поверхностей. Значит, чем лучше отполированы поверхности, тем лучше они будут скользить друг по другу и тем меньше будет сила трения между ними. Можно ли отполировать так, что сила трения вообще будет равна нулю? В какой-то момент неровности станут настолько незначительными, что в контакт придет огромное количество частиц двух поверхностей, а не только частицы шероховатостей, и эти все частицы будут взаимодействовать и препятствовать движению. Получается, что есть предел, до которого сила трения уменьшается при полировке поверхностей, а затем количество взаимодействий между частицами, а поэтому и сила трения, увеличивается. Поэтому мы иногда замечаем, что слишком гладкие поверхности «слипаются».

---

Для тел из одних и тех же материалов сила трения при качении будет меньше, чем сила трения скольжения. Люди знали это уже давно, поэтому придумали колесо.

Но какое бы трение ни было, сила трения направлена в сторону, противоположную относительному смещению поверхностей. Причём направлена она вдоль линии, по которой тела соприкасаются.

---

 

«Разные виды трения»

Существуют разные виды сил трения.

Например, на столе лежит тяжёлая книга. Для того, чтобы ее сдвинуть, потребуется некоторое усилие. И если на книгу нажать слишком слабо — она не тронется с места. Мы же прикладываем силу, почему нет ускорения? Силу, с которой мы толкаем книгу, уравновешивает сила трения между нижней обложкой книги и столом. Эта сила трения препятствует твёрдым телам приходить в движение. Поэтому она называется силой трения покоя.

Сила трения покоя направлена также против движения — того движения, которое только ещё должно было бы возникнуть:

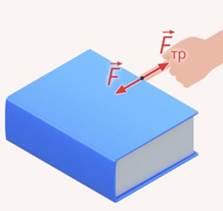
Рис. 7. Сила трения покоя

Чтобы сдвинуть что-то с места, нужно приложить силу, которая больше максимальной силы трения покоя.

При движении жидкости или газа, отдельные слои этих веществ движутся один относительно другого. Между ними возникают силы внутреннего или вязкого трения.

При небольшой скорости течения, в отсутствие вихрей, течение жидкости будет происходить послойно. То есть, жидкость можно мысленно разделить на параллельные слои, каждый слой имеет свою скорость. Слой, находящийся непосредственно у дна, будет неподвижен. Следующий слой будет «скользить» по неподвижному слою. Затем слой с еще большей скоростью относительно дна, скользящий по предыдущему, и т.д. (см. рис. 8). И таким обра